为了有效的使用功率器件,有必要了解规格书中的栅极电荷信息。栅极电荷信息一般出现在规格书的两个位置:一、在动态特性的表格中;二、在特性图中展示栅源电压与总栅极电荷特性曲线。本文说明针对MOSFET,但也同样适用于IGBT。
(一) 栅极电容与电荷基本概念
图1展示了MOSFET等效模型,总栅极电阻RG,寄生电容CGD, CGS, CDS,负载阻抗ZL。
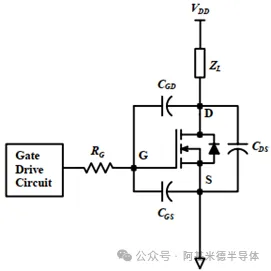
图 1 功率MOSFET模型
图2是规格书中的栅极电荷曲线,它显示栅源电压与注入栅极的电荷的函数关系。只要栅极驱动电流流入栅极,电荷就会在栅极中积累。需要注意的是在该函数关系中VDD是一个参量,图1展示了VDD施加的位置。对于不同的VDD值,达到特定栅极电压所需的电荷是不同的。对于给定的VDD,如果将一定数量的电荷注入栅极,电压将上升到一定水平。本文重点介绍充电过程,因为放电过程可以看作充电的反过程。对于特定的电路,采用不同的驱动器以满足不同的充放电要求,但涉及的物理原理是相同的。
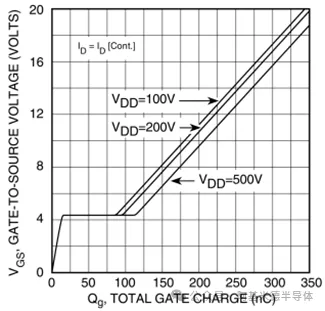
图 2 VGS关于栅极电荷函数(@APT Application Note - October 31, 2001)
如图3所示,Qgs是曲线中从原点到第一个拐点的电荷,Qgd是曲线中第一个拐点到第二个拐点的充电电荷,Qg是从原点到曲线上VGS等于峰值驱动电压的点的电荷。
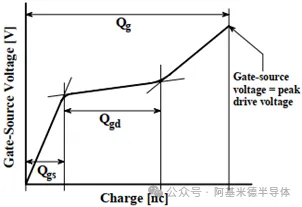
图 3 VGS关于栅极电荷函数(@APT Application Note - October 31, 2001)
图4展示了规格书中的电容曲线,是VDS的函数:Ciss是输入电容,Coss是输出电容,Crss是反向传输电容。就图1模型中的端子间电容而言,Ciss=CGS+CGD,Coss=CDS+CGD和Crss=CGD。Ciss、Coss和Crss随VDS而变化,因为CGD和CDS随VDS的变化而变化。
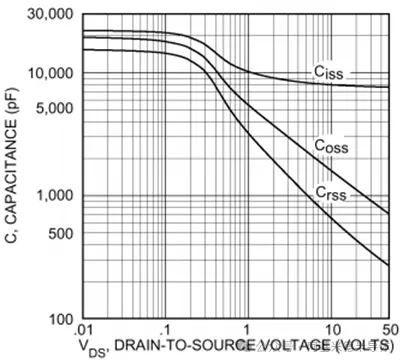
图 4 典型电容关于vDS的函数(@Infineon Datasheet)
而CGS是恒定的,如图5所示。通过CGD和CDS的电流取决于电容与其电压乘积的时间导数。
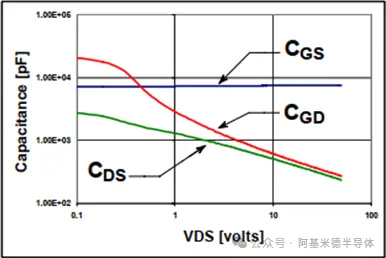
图 5 端子间电容关于vDS的函数(@APT Application Note - October 31, 2001)
图3展示了VGS关于栅极电荷的函数。当测量实际完成后,VGS可以作为时间函数绘出,如图6所示,通过时间与电荷的关系两条曲线可以互相转换。在栅极电荷测量中采用恒流栅极驱动。为了确定有多少电荷被注入到栅极中,需要对进入栅极的电流进行积分。对于任何给定的时间段,从该时间段的开始到结束对栅极电流进行积分,决定了在此期间注入栅极的电荷量。如果我们用iG表示栅极电流,Q表示进入栅极的电荷,tb(开始时间)和te(结束时间)表示时间段,方程如下:
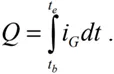
当采用恒定电流源时,该方程等效为:
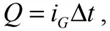
其中Δt为恒定电流的积分区间,即te-tb.通过该简化方程,栅极的恒定电流源可以将电压与时间曲线转化为电压与电荷曲线。此外漏极中的恒定电流消除了测量中引线电感的影响。
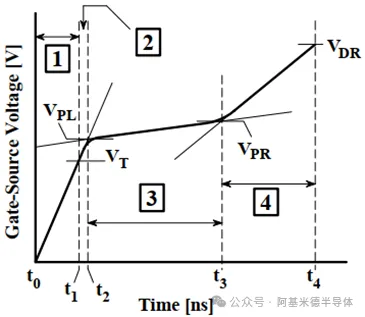
图 6 vGS关于时间的函数(@APT Application Note - October 31, 2001)
图6中的四个时间段由VGS和VGD的特征变化来描述。其中t=t0为原点,VT为阈值电压,VPL为VGS中平台的左端,VPR为同一平台的右端,以及VDR——驱动电压的峰值。当驱动电路是电压源时,该峰值是驱动器输出端的标称电势。然而,如图6所示,当采用恒定的栅极电流时,驱动器是一个电流源,栅极电压的峰值被选择为10V,如数据表所述。在栅极电压的峰值处确定总栅极电荷。
(二) 开通过程栅源电压上升的四个阶段
图6中的四个时间阶段将在下文中详细介绍。虽然将充电时间分为四个时段有助于对栅极电荷的理解,但数据表使用前面提到的三个电荷量来描述。图7显示了MOSFET在导通时的开关波形。图7中的时间尺度为us而不是ns,因为设置的栅极驱动恒流源为较小的量级(1mA),这是测量栅极电荷的标准方法,在该方法中的测试负载为恒流源。
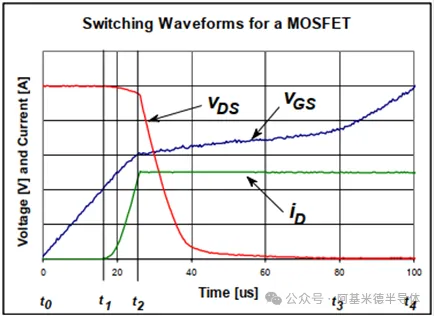
图 7 开通曲线(@APT Application Note - October 31, 2001)
1. 从0至VT(t0至t1)
VGS从0上升至VT;
iD为0;
VDS无变化。
当VGS在这个值范围内时,0<VGS<VT,MOSFET未开启,VDS恒定在电源电压VDD的电平。在时间t=t0,当施加恒定栅极电流时,VGS开始上升。VGS的上升是由CGS和CGD的充电引起的。认为在这种状态下只有CGS被充电是一种误解,因为如果栅极节点的电势上升,那么CGD两端的电压就会发生变化,这需要电荷流入CGD。在VDS值不变的情况下,CGS比CGD大得多,因此流入CGS的驱动电流比流入CGD的驱动电流大得多。当VGS= VT在t = t1时,这段时间内VGS的上升结束。到目前为止,漏极电流还没有开始流动。需要注意的是,CGS不是电压的函数,而CGD是。因此,在这段时间内,CGS是恒定的,但CGD略有增加,这可以从图5中理解。
2. 从VT至VPL(t1至t2)
VGS由VT上升至VPL;
iD开始流动;
VDS开始降低;
Qgs是从时间t0到时间t2注入栅极的电荷。
阈值电压定义为iD开始流动的栅源电压。忽略掉低电平、阈值前的电流。因此在t = t1时,iD开始流动,VDS开始以一定的变化率下降。时间周期在t = t2处结束,第一个拐点出现。
拐点的产生取决于产品CGD·VGD随时间的变化率。更一般的电容电流表达式在这里适用,因为电容CGD是变化的。由于q = Cv,电容器中的电流方程是:
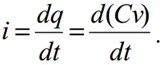
这是当C和v都随时间变化时必须使用的表达式。VGD= VGS - VDS,是iD和ZL的函数。任何iD和ZL的组合,使VDS下降得足够快,进而导致VGD增加,将导致拐点。如前所述,VGD增加意味着它变得不那么负了。理论上,iD实际上在左拐点发生后才会达到最大值,因为CGD中的电流d(CGD·VGD)/dt决定了左拐点的发生。较小的iD值和较大的ZL值可以实现这一点。
3. 从VPL到VPR(t2至t3)
VGS从VPL逐渐上升至VPR;
在某个时刻,iD达到最大值;
VDS在t3时达到最小值;
Qgd是从t2到t3时间段内注入栅极的电荷。
当VGS继续上升直至超过阈值电压VT和平台电压VPL,由于栅极电流转移的电荷的影响,VGS的斜率将显著降低(甚至降低到零)。此时,VGS进入平台区,如图6中的t = t2所示。严格意义上,VGS 平台区的斜率取决于栅极驱动电流在栅-漏电容CGD和栅-源电容CGS之间的分配,而这种分配进一步取决于测试条件或电路条件。如果上升得足够快,平台区的VGS将保持恒定:VGS= VPL =VPR。在这种状态下,VGS斜率为零而持续增加,意味着没有任何驱动电流流入CGS,全部的驱动电流用于增大CGD两端的电压降。如果VGS斜率非零,则意味着部分驱动电流流入了CGS,导致VGS以较慢的速率上升。
在第一和第二时间段内,一部分驱动电流无法避免地流入CGD;然而在第三时间段,通过提供足够的负载阻抗和足够大的输入电阻,有可能使几乎所有的驱动电流流至CGD。也就是说,平台区的斜率取决于CGS、CGD 以及驱动和负载电路元件。然而,无论VGS平台区的斜率如何,当MOSFET完全导通时,到达t3时刻。
在整个第三时间段内,VDS持续下降(意味着VGD上升),同时 CGD增加。当VDS下降到时,VDS停止下降,CGD也停止增加。这里ID 的大写 “I” 表示漏极电流 iD的峰值已经到达,标志着第三时间段的结束,vGS开始以一个新的更高的速率上升。当vGS = VPR 且t = t3 时,到达VGS平台区的右端。
4. 从VPR到VDR(t3至t4)
VGS从VPR逐渐上升到VDR;
iD保持最大值;
VDS保持最小值;
Qg是从t0到t4时间段内注入栅极的电荷.
当VDS降至最小值时,VGS退出平台区,并以一个新的速率上升。此时,由于VDS不变,绝大部分的驱动电流再次流入CGS,但斜率比第一个时间段小,因为此时CGD比第一个时间段大得多,且其值接近CGS。
参考文献:
[1] “Use Gate Charge to Design the Gate Drive Circuit for Power MOSFETs and IGBTs.”AN-944. International Rectifier.
[2] Grant, Duncan A. and John Gowar. POWER MOSFETS Theory and Applications, p. 84. New York: John Wiley & Sons, 1989.
[3] Pressman, Abraham I. Switching Power Supply Design, Second Edition, pp. 359-361. New York: McGraw-Hill, 1998.
[4] Erickson, Robert, Bill Behen, R. D. Middle brook, and Slobodan Ćuk. “Characterization and Implementation of Power MOSFETs in Switching Converters.” In Proceedings of Powercon® 7, pp. 188-189. The Seventh National Solid-State Power Conversion Conference, March 24-27, 1980, San
[5] Diego, California. Power Concepts, Inc., 1980.
[6] Department of Defense Test Method Standard, Semiconductor Devices, Mil-Std 750D, February 28, 1995, Method 3471.
[7] Dierberger, Kenneth. “Gate Drive Design for Large Die MOSFETs.” Application Note APT9302. Advanced Power Technology.
| 上一篇:解读SiC MOSFET关键参数——Vth | 下一篇:浅谈多并联SiC MOSFETs不均流问题 |
安徽省合肥市高新区长宁大道789号5号楼



